Planning and Managing Distance Education Systems: System Modeling
Farhad Saba, Ph. D.
Founder and Editor, Distance-Educator.com
In this series of articles, I presented a hierarchical model of distance education consisting of seven interrelated nested systems levels. These systems have been present in most distance education organizations that I observed, or planned and built over the past 30 years. In the previous weeks, I discussed Hardware, Software, Telecommunications, Instructional, Educational, Societal and Global Systems Levels. In this article the process of modeling will be explained in further detail so that you could start the planning process for your organization. I hope that conducting the environmental scan as presented in the previous article has given you a better appreciation of the components of the technology-based educational programs in your organization and the interrelationships among such components. We also hope that you realize that the environmental scan can be an iterative activity, and as you learn more about the modeling process, you would be able to develop more comprehensive models of your organization by reviewing the components and processes involved in your institution. Keep in mind that each institution is unique and the purpose of learning the modeling process is to create a unique plan for the future development of your institution as no one model or solution can be developed and applied to all institutions.
Systems methodology is a means of analyzing parts of a whole and understanding the relationships among them in formal mathematical language.
As an introduction to the modeling process, a simple distance education system is presented in this chapter in more detail. This will include:
- Problem definition
- System conceptualization
- Model representation
- Model behavior
- Model evaluation
- Policy analysis and model use
System Methodology for Modeling
Systems methodology is a means of analyzing parts of a whole and understanding the relationships among them in formal mathematical language. This process of analysis and synthesis is based on a set of principles that have developed over the years. The characteristics of systems, outlined in the side bar, are a summary distilled from some of the significant contributors to the field of systems analysis and organization development. (Akoff, 1979; Anderson & Johnson, 1997; Banathy, 1992; Bertalanffy, 1988; Capra, 1982, 1996; Churchman, 1979; Dubin, 1978; Lazlo, 1996; Prigogine, 1997; Roberts et al., 1983; Senge, 1990; Skyttner, 2001).
The human body is a good example of a system. Different organs of the body work together, but they cannot function in isolation. What the body does as a whole is always greater than the sum total of its parts. In other words, humans are capable of sustaining life and thinking in abstract, which has enabled them to develop schools of philosophy, create literature, devise technologies, and change their environment in so many different ways.
Components of a system can be:
- People- e.g., instructors, learners, administrators, policy makers , politicians and employers;
- Objects- e.g., computers and telecommunication lines that make communication among the people possible, and
- Intangibles- e.g., laws, rules, policies and procedures that govern how people and objects function in society, in an organization or in a family.
System Boundary– A system can be composed of any number of these components that work together to make up a school, a university, an extended studies division, an academic department in a college or a distance education program. In the planning process the modelers in institutions of higher education might consider these types of organizational units to define the boundary of a system and decide which components should be included in a model. All necessary components must be included in a model for a system to reach its goal but it should not include any unnecessary components.
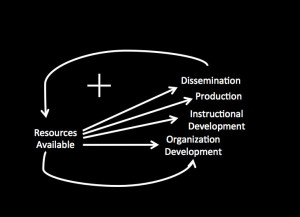
Figure 1- Causal loop diagram of a simple model of a distance education system adapted from Saba, and Twitchell 1988.
Saba and Twitchell (1988) developed an example of a very simple system representing selected components of a distance education system to demonstrate the application of systems approach to modeling for distance education organizations. The components for this model were selected from a study of twelve educational broadcasting organizations in Africa, Asia and Europe as well as North and South America by Hawkridge and Robinson (1982). These components presented in the following causal loop diagram in Figure 1 were present in all of the organizations that Hawkridge and Robinson studied. The causal loop diagram also identifies the relationships among these components by feedback loops.
The purpose of the simulation study was twofold: First it was to find out if the initial number o f students enrolled in a distance education system affected the resources allocated to the system? In other words, were there an optimal number of students necessary to generate enough income in a distance education system to make it viable in the long run? Second, the study was to determine how do resources available to a system affected the performance of each system function?
the study focused on resources available to an organization that can be spent on organizational and instructional development, production of instructional materials and dissemination of courses to support a certain number of enrollments.
Put differently, the study focused on resources available to an organization that can be spent on organizational and instructional development, production of instructional materials and dissemination of courses to support a certain number of enrollments. Dissemination of courses in the model leads to enrollments as well as graduates and dropouts. At each point in time student population depends of the number of enrollments minus those that have graduated or dropped out. At each point in time student population determines the resources available to the systems at which point the causal loop repeats itself. This model was run several times based on different assumptions in terms of initial dollar amounts of resources available in order to determine the level of student population which would make the system sustainable based on its income from dissemination of courses. Undoubtedly distance education systems in operation in colleges and universities have more components and are more complex than this model. However, as an initial study in 1988, the objective here was to define the boundary of the system so that it would include a small but sufficient number of components. As it turned out, even this small model had to be expanded a bit to make it operational on a computer. The details of this expansion will be explained as I describe the process of model building in the next article.








